El método simplex existe desde la segunda guerra mundial y consiste en un algoritmo matemático, que mediante iteraciones secuenciales se va aproximando a una solución optima a un problema de programación lineal. Se utilizará el método simplex para resolver problemas en los que se deba maximizar o minimizar una variable. Actualmente se utiliza mucho en la administración de empresas y la ingeniería industrial para maximizar la producción y minimizar costos en distintos sectores.
A continuación, presentaremos un ejemplo sencillo de introducción, en video, de cómo se utiliza el método simplex, utilizando Excel para solucionar un problema de transporte. Pero antes vamos a definir bien algunos términos.
Vamos a citar a continuación el libro “Métodos cuantitativos para los negocios” de Anderson y otros:
Índice de contenidos
Programación Lineal
La programación lineal es un método de solución de problemas desarrollado para ayudar a los gerentes a tomar decisiones. En el competitivo entorno de negocios actual pueden encontrarse varias aplicaciones de programación lineal. Por ejemplo, Eastman Kodak utiliza la programación lineal para determinar dónde fabricar productos en sus instalaciones de todo el mundo, y GE Capital la utiliza para determinar la estructuración de arrendamiento óptima. Marathon Oil Company utiliza la programación lineal para la mezcla de gasolina y evaluar la economía de una nueva terminal o tubería de distribución. El artículo de MC en acción, “Modelo de recolección de árboles en MeadWestvaco Cor poration”, proporciona otro ejemplo del uso de la programación lineal. Después, el siguiente artículo de MC en Acción ilustra cómo Hanshin Expressway Public Corporation utiliza la programación lineal para el control de tráfico en una autopista de cuota urbana en Osaka, Japón.
Para ilustrar algunas de las propiedades que tienen en común todos los problemas de programación lineal, considere las siguientes aplicaciones típicas:
1. Un fabricante quiere elaborar un programa de producción y una política de inventario que satisfaga la demanda de ventas en periodos futuros. En términos ideales, el programa y la política permitirán a la empresa satisfacer la demanda y al mismo tiempo minimizar los costos totales de producción e inventario.
2. Un analista financiero debe seleccionar un portafolio entre diversas alternativas de acciones e inversiones. Al analista le gustaría establecer el portafolio que maximice el rendimiento sobre la inversión.
3. Un gerente de marketing quiere determinar cómo asignar mejor un presupuesto de publicidad fijo entre medios de publicidad alternos como la radio, la televisión, el periódico y las revistas. Al gerente le gustaría determinar la combinación de medios que maximice la efectividad de la publicidad.
4. Una empresa tiene almacenes en varias ubicaciones. Dadas las demandas específicas de los clientes, a la empresa le gustaría determinar cuánto debe enviar cada almacén a cada cliente, de modo que los costos del transporte local se minimicen.
Estos ejemplos son sólo algunas de las situaciones en las cuales la programación lineal se ha utilizado a satisfacción, pero ilustran la diversidad de las aplicaciones de la programación lineal. Un escrutinio meticuloso revela una propiedad básica que tienen todos en común. En cada ejemplo nos interesa la maximización o minimización de alguna cantidad.
«Métodos cuantitativos para los negocios»; Anderson, Sweeney, Williams, Camm, Martin. 2011 Pág.235
Ejemplos de Programación Lineal
En el ejemplo 1, el fabricante quería minimizar los costos; en el ejemplo 2, el analista financiero quería maximizar el rendimiento sobre la inversión; en el ejemplo 3, el gerente de marketing quería maximizar la efectividad de la publicidad, y en el ejemplo 4, la empresa quería minimizar los costos de transporte totales. En todos los problemas de programación lineal, el objetivo es la maximización o minimización de alguna cantidad.
«Métodos cuantitativos para los negocios»; Anderson, Sweeney, Williams, Camm, Martin. 2011 Pág.235
Programación Lineal con Método Simplex – Ejemplo
Vamos a ejemplificar como utilizar el método simplex para resolver un problema de programación lineal, utilizando Excel. El ejercicio lo puede encontrar en la página 419 del libro citado, y es el que mostramos a continuación:
Problema de Transporte
El problema de transporte surge con frecuencia en la planeación de la distribución de productos y servicios desde varios sitios de suministro hacia varios sitios de demanda. La cantidad de productos disponibles en cada locación de suministro (origen), por lo general, es limitada, y la cantidad de productos necesarios en cada una de varios sitios de demanda (destinos) es un dato conocido. El objetivo usual en un problema de transporte es minimizar el costo de enviar mercancía desde el origen a sus destinos.
Ejemplifiquemos esto al considerar el problema de transporte que enfrenta Foster Generators. Este problema implica el transporte de un producto desde tres plantas a cuatro centros de distribución. Foster Generators opera plantas en Cleveland, Ohio; Bedford, Indiana, y York, Pennsylvania. Las capacidades de producción durante el próximo periodo de planeación de tres meses para un tipo particular de generador son las siguientes:

La empresa distribuye sus generadores a través de cuatro centros de distribución regionales localizados en Boston, Chicago, St. Louis y Lexington; el pronóstico de la demanda en los tres meses para los centros de distribución es el siguiente:

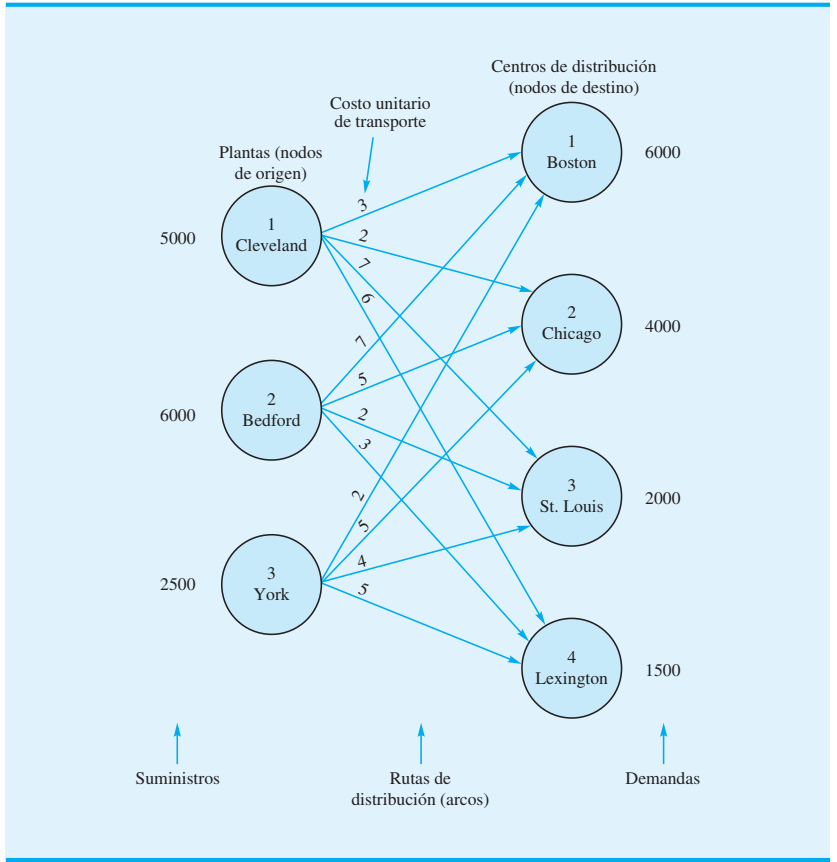
A la gerencia le gustaría determinar cuánto de su producción debe enviarse desde cada planta a cada centro de distribución. La figura 10.1 muestra las 12 rutas de distribución que Foster puede utilizar. Una gráfica como ésta se llama red; los círculos se conocen como nodos y las líneas que conectan los nodos son los arcos. Cada origen y destino se representan por medio de un nodo y cada ruta de envío posible se identifica mediante un arco. La cantidad del suministro se escribe al lado de cada nodo de origen y la cantidad de la demanda se escribe al lado de cada nodo de destino. Los productos embarcados desde los orígenes a los destinos representan el flujo en la red. Observe que la dirección del flujo (desde el origen al destino) se indica mediante flechas.
Para el problema de transporte de Foster, el objetivo es determinar las rutas y la cantidad que se enviará por cada una de ellas para lograr que el costo total de transporte sea mínimo. El costo para cada unidad embarcada en cada ruta se proporciona en la tabla 10.1 y se muestra en cada arco de la figura 10.1.

La solución que le dimos se expresa en el presente video:

Deja una respuesta